MOL Comfort- What Happened? (Part 2)

Flashback

In Part 1, we focused on the position of the crack on the hull girder, following which we saw how Class NK estimated the wave induced loads on the ship during the accident scenario, considering required uncertainties in the parameters. Based on the above obtained wave loads for different sea states, the maximum and minimum wave induced vertical bending moments were estimated.Having estimated the wave induced load, it was now required to estimate the hull girder strength (of the considered three hold model). This article is about to discuss the methods involved in calculating the strength of the structure, and obtained results of the same.

3-Hold Model for Strength Analysis

The region of failure was identified by field investigations. So for the finite element analysis, a three hold model was considered. Further conditions taken during the analysis were obtained from Class NK Guidelines for Container Carrier Strength (Guidelines for Direct Strength Analysis, 2012) as shown in Table 1.

Table 1: Conditions for 3-hold model analysis.
(Courtesy: Class NK)

Fig. 1: 3-hold model used for analysis. (Photo edited)
(Courtesy: Class NK)

Estimation of Ultimate Strength

The strength of the three hold model was estimated considering uncertainties as shown in Figure 2.

Fig. 2: Factors affecting uncertainty in strength of the double bottom structure.

How was the yield stress of the structure calculated? The value of yield stress of the members were obtained from their respective mill sheets. The average of all the yield stress values of the different member materials were calculated and regarded as the mean value of hull girder ultimate strength (μ).

It is important to understand what was done next. Given the fact that the strength of a marine structure follows a probabilistic nature (that can be represented by a Probability Density), it is evident that consideration of mean value alone for determining the ultimate structure is not a valid thing to do. What if the strength of the structure at any point of time, reduces from its mean value? Therefore, it is necessary to determine the minimum ultimate strength of the structure to consider the worst case scenario.

Class NK adopted two different methods to determine the minimum hull girder ultimate strength, an the strengths obtained through each of the two methods were categorized as Case 1 and 2 (will be referred by the same hereinafter).

Case 1- The standard deviation (σ) of the yield strength of the bottom shell plates were calculated from the mill sheet values. The minimum yield stress of the hull girder was defined as the value that was less than the mean by three times the standard deviation, i.e. Minimum yield stress = μ-3σ (Refer to Figure 3)
The hull girder ultimate strength was then evaluated corresponding to the above minimum yield stress of the bottom plating. This ultimate strength was regarded as the minimum hull girder ultimate strength.

Fig. 3: Graphical representation of Case 1

Case 2- The hull girder ultimate strength was evaluated corresponding to the minimum yield stress of the bottom plating specified in the mill sheets. The obtained ultimate strength was then regarded as the minimum hull girder ultimate strength.
The obtained values of yield stress (for both the cases) were as shown in Table 2.

Table 2: Yield stress for Case 1 and Case 2.

Now, in order to find the ultimate strength, a very simple method was adopted: The loads at the time of the accident were known and categorized into the following:

1. Hull weight corresponding to the double bottom structure (known before analysis)
2. Hydrostatic pressure corresponding to the full draught (known before analysis)
3. Container Loads (known before analysis, based on the loading information at the time of the accident)
4. Allowable still water bending moment for hogging (calculated before the analysis, from loads 1, 2 and 3)
5. Wave-induced pressure (priorly calculated from Class NK Direct Strength Analysis, 2012)
6. Wave-induced vertial bending moment (calculated from IACS UR S11)
7. Additional vertical bending moment (due to uncertainties)

The interesting part is how these loads were applied to the model for analysis. Initially, loads 1,2, and 3 were gradually increased every one second until they reached their known values. Then loads 4, 5, and 6 were applied in turn and increased every one second until their known values were attained. At last, load 7 was gradually increased every second until the stress in the structure exceeded the Von Mises Stress of the structure. (Graphical representation in Figure 4). The stress at which the structure failed, was regarded as the Hull Girder Ultimate Strength.

Fig. 4: Sequence of application of load on the model.
(Courtesy: Class NK)

The above method was followed for three conditions:

1. When yield strength of the structure was corresponding to the mean value (μ)
2. Case 1: Yield strength = μ-3σ
3. Case 2

The hull girder ultimate strength was also obtained for three different conditions and the corresponding vertical bending moments were obtained, as shown in Table 3.

Table 3: Obtained values of Vertical Bending Moments when the hull girder fractured.

Fig. 5: Time vs. Bending moment at the section that suffered failure in the case of average yield stress. (Picture edited)
(Courtesy: Class NK)

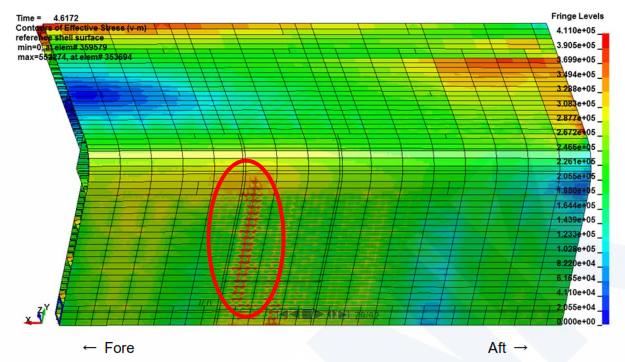Fig. 6: Von Mises stress at the time of peak load.
(Courtesy: Class NK)

Fig. 7: Equivalent plastic strain at the time of peak load.
(Courtesy: Class NK)

Fig. 8: Von Mises stress at the time of peak load.
(Courtesy: Class NK)

Fig. 9: Equivalent plastic strain at the time of peak load.
(Courtesy: Class NK)

What's in Part 3?

Certain factors were multiplied to the obtained values of bending moment, in order to compensate for the factors of local deformations and residual stresses due to welding. Inclusion of these factors, reduced the strength further. It is on the basis of the then obtained strength values, that the probability and extent of damage will be discussed in the next part of this series.LSD

Article By: Soumya Chakraborty